
La ZAC est-elle une sorte d’ignominie proliférant comme un virus inventé par un docteur Folamour de l’architecture ? Les mathématiques semblent le démontrer.
Le XXe siècle a été riche en outils d’analyse de la ville. Nombreuses sont les sciences qui l’ont permise. Il fut question de morphologie urbaine, de typologie urbaine et même de typo-morphologie. Architectes et historiens se sont penchés sur le décryptage de l’urbain et, de Jean Castex à Pierre Pignon en passant par Philippe Panerai, j’en oublie sûrement, ils ont identifié les différents éléments constitutifs de la structure complexe de la ville.
L’identification des réseaux, des trames viaires, des trames bâties, des vides et des jardins, etc. a permis l’élaboration de manuels exhaustifs des éléments qui peuvent exprimer la forme urbaine. La superposition, et non la juxtaposition, de ces systèmes complexes rend compte de la ville tel que nous la percevons.
Qu’en est-il des usages et de la pratique des espaces inhérents à la forme urbaine ? L’identification des strates ne renvoie pas à l’usage. La question du «point rencontre» entre ces différentes structures urbaines est le phénomène déterminant qui permet de passer de la forme à la valeur d’usage et ainsi de s’affranchir de l’espace géométrique.
Si l’on devait appliquer ces outils d’analyse de la forme urbaine à des villes comme Paris, New York, Tokyo, elles révéleraient leurs spécificités renvoyant à des usages inhérents à leur forme urbaine respective. A l’heure d’internet, des réseaux sociaux, de McDonald’s et de Starbucks café, aucune de ces villes n’est devenue un modèle universel répété à l’envi.

D’autres approches de la morphologie urbaine ont donné lieu à des réflexions alternatives comme le montre feu Benoît Mandelbrot, l’inventeur des Fractales. Le terme «fractale» est un néologisme créé par le mathématicien franco-américain à partir de la racine latine du mot fractus, qui signifie «brisé», «irrégulier». Il étudie le tracé des lignes de côtes, notamment des côtes bretonnes, et démontre que, dans l’infinitésimal, il existe un ordre dans certains systèmes dont la complexité semble pourtant impénétrable.
René Thom, mathématicien et auteur de la théorie des catastrophes, entre autres, a également écrit un ouvrage sur la stabilité structurelle et la morphogenèse. Il explique qu’il y a de la «continuité» dans ce qui est considéré a priori comme des éléments de «discontinuité».
Cette digression amène à questionner les formes urbaines développées depuis ces trente dernières années. Il n’est pas question de la ville nouvelle de Paul Delouvrier mais de la ville des ZAC, «Zone d’Aménagement Concerté». Ce modèle, devenu universel, se retrouve de Boulogne Billancourt à Montpellier, de Toulouse à Lilles en passant par la Chine.
Un modèle à l’architecture généreuse, aux espaces publics qui se développent à l’infini, ou le paysage – ah ! le paysage – y est plus vrai que nature, au plus loin de l’approche du paysage chère à Michel Corajoud.
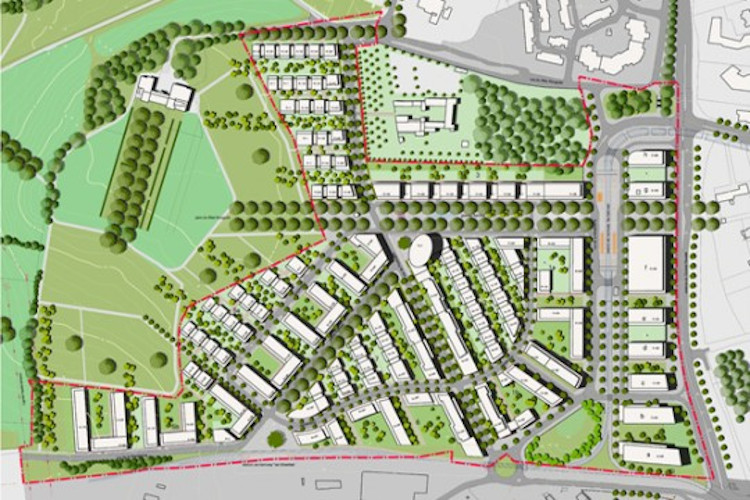
A quoi nous renvoie l’acronyme ZAC ? La ZAC constitue une procédure d’initiative et d’intérêts publics, même si sa réalisation est susceptible d’être confiée à un aménageur privé et à des promoteurs privés. Elle s’utilise essentiellement pour des opérations d’une certaine envergure. Une même zone d’aménagement concerté peut être créée sur plusieurs emplacements territorialement distincts. Il s’agit alors d’une ZAC multi sites.
La ZAC est le mot savant pour évoquer la ville et son développement. Un modèle urbain économiquement approuvé, dont sa forme urbaine est éprouvée.
Loin de retrouver les liaisons complexes engendrées par la superposition de réseaux, la ZAC est la juxtaposition d’éléments morphologiques simples dont il est possible de dresser une liste exhaustive : voie, stationnement, trottoirs bordés d’arbres, forme du bâti régulière, jardin, square, sans oublier les noues pour l’évacuation des eaux pluviales pour faire «Ecoquartier».

Il est simple de comprendre pourquoi ce modèle urbain se retrouve en Chine, puisque le site et son environnement quels qu’ils soient ne sont plus des éléments de réflexion contextuelle et spécifique. A y regarder de plus près, le plan voisin de Le Corbusier, où l’on retrouve des éléments de la morphologie urbaine devenus des types, n’est pas très loin.

Dans son livre Prédire n’est pas expliquer, René Thom explique que «prédire, c’est extraire d’une connaissance du passé une connaissance de l’avenir». L’intérêt de cette citation est que, sortie de son contexte mathématique, elle peut s’appliquer tout aussi bien au monde réel avec une approche purement pragmatique.
Le plan voisin cher à Le Corbusier est une connaissance du passé qui a tout du réel : la ZAC !
Gemaile Rechak